







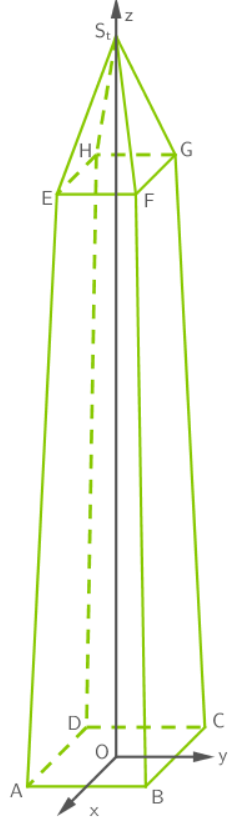
Die Abbildung zeigt ein Modell eines Obelisken. Im verwendeten kartesischen Koordinatensystem (1 Längeneinheit entspricht 1 Meter) beschreibt die xy-Ebene den ebenen Untergrund, auf dem der Obelisk steht. Das Modell des Obelisken besteht aus zwei Teilkörpern. Der untere Teilkörper ABCDEFGH mit B (0,45 | 0,45 | 0,00) ist ein Stumpf einer geraden Pyramide. Dieser Stumpf entsteht, indem man von einer geraden Pyramide mit einer quadratischen Grundfläche parallel zur Grundfläche eine kleinere Pyramide abschneidet. Die Grundfläche ABCD des unteren Teilkörpers liegt in der xy-Ebene, der Mittelpunkt des Quadrats ABCD ist der Koordinatenursprung. Der obere Teilkörper EFGHSt mit E (0,35 | -0,35 | 7,16) ist eine gerade Pyramide mit der Spitze St (0,00 | 0,00 | 7,16+t) mit tϵR und t>0. Abb. 1: nicht
maßstäblich
|
 |

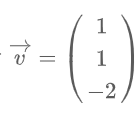 dargestellt.
Für diesen Fall gibt es
Werte von t, so dass die Spitze St des
dargestellt.
Für diesen Fall gibt es
Werte von t, so dass die Spitze St des